深度学习任务的核心

• 按照目标场景的需要去理解“世界”

这是何物第二关

这是何物第三关

理解世界的方式

• 人如何理解世界: 通过外延观察=>自动构建内涵

• 内涵: 一个概念的内涵是指它的“内容”或“定义”，即该概念所包含的性质、特征或条件

  • “人”: 有理性、社会性和自我意识的生物

• 外延: 一个概念的外延是指它所指代的所有对象的集合，或者说它所涵盖的实际事物的范围

  • “人”: 是所有的人类个体，如亚里士多德、牛顿、爱因斯坦

模型学习的核心

模型如何理解世界: 通过外延观察=>自动构建内涵

• 模型理解世界的过程
  • 设定任务目标
  • 收集外延: 数据集
  • 构建内涵: 学习特征

深度学习的特点

表示学习(representation learning)

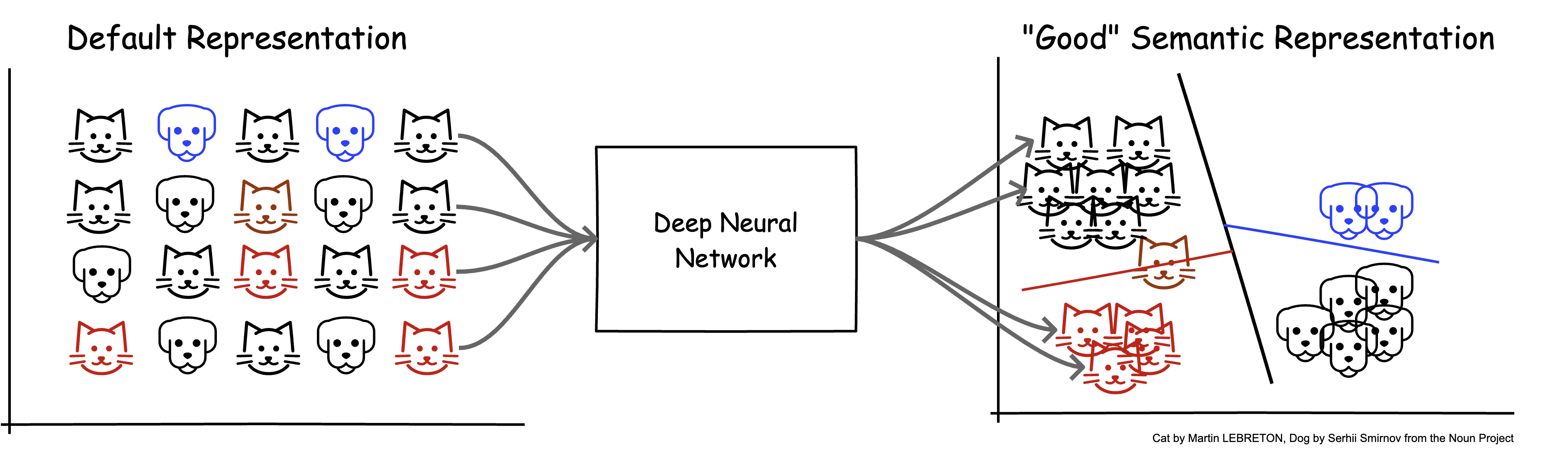
深度学习模型

深度学习模型

典型结构

• 前n-1层(堆叠)
  • 输入: 特征表示
  • 输出: 特征表示
• 第n层
  • 输入: 特征表示
  • 输出: 任务目标

深度学习模型的线性层

• 和: 特征表示
  • : 当前层输入/前一层输出
  • : 当前层输出/后一层输入
• : 当前层参数
  • 表示空间变换函数

线性层的计算

输入：b个样本，每个样本表示在一个d维的空间中
函数：函数将表示在d维空间中的样本变换到e维的空间中
输出：的输出，b个样本，每个样本表示在一个e维的空间中

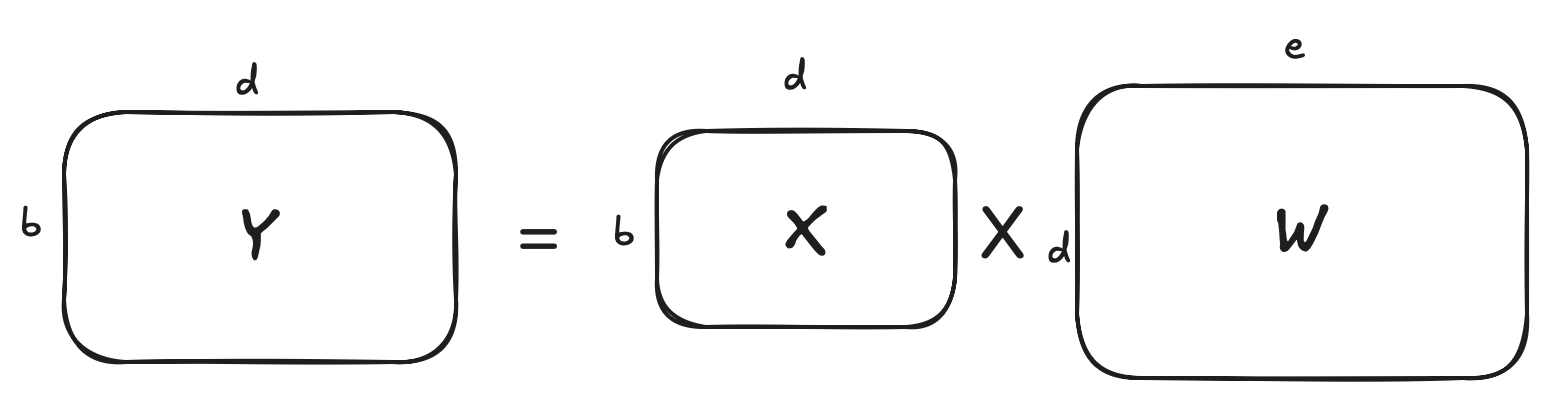
空间变换的具体实现

理论上：运用线性代数中的矩阵乘法

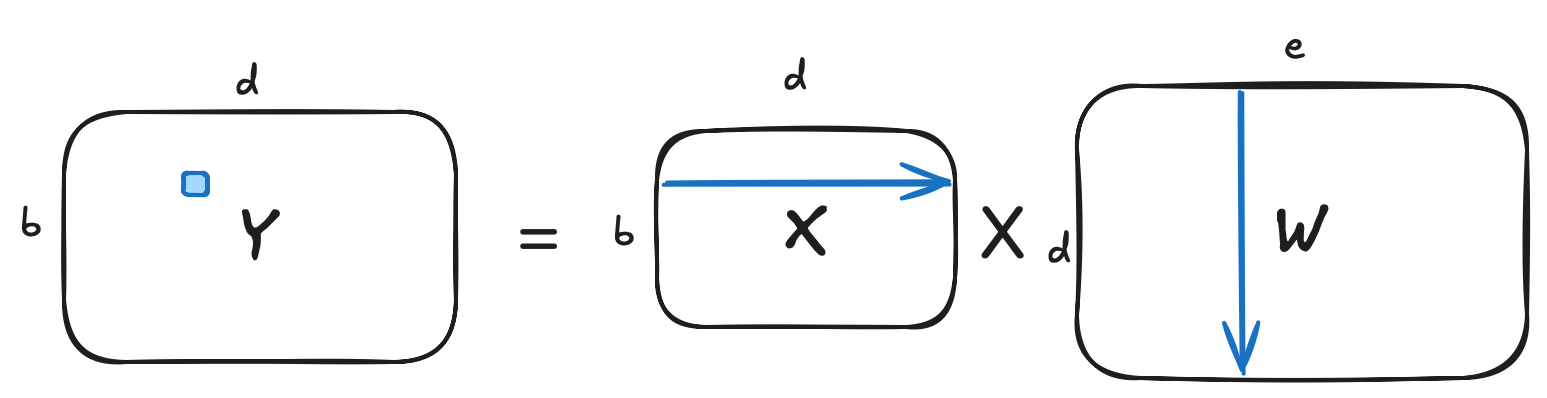
矩阵乘法的复杂度分析

• 计算 时，每个元素 是一个 点积：

• 每个 需要 次乘加运算
• 总共有 个元素，
  

矩阵乘法的优化思路

• 内存局部性 (Blocking)
  • 数据按小块（tile）加载到cache中，避免反复访问大矩阵
• 向量化计算 (Tiling)
  • 一次处理多个数据 (SIMD/SIMT)，例如一次性做 8 个乘加
• 并行化
  • 多核CPU：不同线程处理不同矩阵块
  • GPU：上万线程同时处理小块矩阵

PyTorch手搓乘法

承载数据的基本类型：Tensor。那什么是 Tensor？

• Tensor可理解为多维数组
• 在 PyTorch 中是最基础的数据结构
• 类似 NumPy 的 ndarray，但有两个关键特性：
  • 支持在GPU上高效计算
  • 支持自动求导(autograd)

Tensor 的维度

• 标量 (Scalar)：0 维张量
• 向量 (Vector)：1 维张量
• 矩阵 (Matrix)：2 维张量，常用与模型参数W
• 高维 Tensor：常用于输入输出(Input/Output)/激活(Activation)

  torch.tensor(3.14)   # shape = []
  torch.tensor([1, 2, 3])   # shape = [3]
  torch.tensor([[1, 2], [3, 4]])   # shape = [2, 2]
  x = torch.randn(2, 3, 4, 5) # shape = [2, 3, 4, 5]

PyTorch手搓乘法

• 操作数有了，那操作符呢？
• 矩阵乘法 (Matrix multiplication)
  • Operator @
  • torch.matmul, tensor.matmul
• 元素乘法 (element-wise multiplication)
  • Operator *
  • torch.mul, tensor.mul
• 高阶的:
  • torch.einsum

编码时间

矩阵乘

y = x@w
y = x.matmul(w)
y = torch.matmul(x, w)

元素乘

y = x*w
y = x.mul(w)
y = torch.mul(x, w)

einsum

• torch.einsum (equation, tensor list)
  • equation: 使用 爱因斯坦求和约定 (Einstein Summation Convention) 描述张量运算 (基于tensor下标)
  • tensor list: input
• 优点：直观，代码可读性强

einsum 表达式

矩阵乘法的数学形式：

einsum 表达式

import torch

X = torch.randn(2, 3)   # B=2, D=3
W = torch.randn(3, 4)   # D=3, E=4
Y = torch.einsum("bd,de->be", X, W)
print(Y.shape)  # torch.Size([2, 4])

批量矩阵乘

• 数学形式：

• einsum 表达式：

A = torch.randn(10, 3, 4)   # batch=10
B = torch.randn(10, 4, 5)

Y = torch.einsum("bik,bkj->bij", A, B)
print(Y.shape)  # torch.Size([10, 3, 5])

构建最基础/核心的模型"积木"

线性层 (torch.nn.Linear):

• torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)

  • in_features: size of each input sample
  • out_features: size of each output sample

• PyTorch中的输入/输出: 都是tensor

  • input:
  • output:

"积木"nn.Linear的要素

self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.empty((out_features, in_features), **factory_kwargs))

• weight: W
  • 与in_features和out_features共同规约了输入输出部分维度的尺寸
  • 实现了从一个空间到另一个空间的变换

"积木"nn.Linear的要素

def forward(self, input: Tensor) -> Tensor:
        return F.linear(input, self.weight, self.bias)

• 计算方法forward: 定义输入到输出的计算过程
  • nn.Linear的forward: 实现

nn.Linear的使用

Torch docs中的官方示例

m = nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)
print(output.size())

新手村之积木堆叠

m1 = nn.Linear(20, 30)
m2 = nn.Linear(30, 40)
x = torch.randn(128, 20)
y1 = m1(x)
y2 = m2(y1)

• 基于nn.Linear实现以下函数组合

思考：这样的输入行么？

x = torch.randn(128, 4096, 30, 20)
y = m1(x)
y = m2(y)

多种多样的积木

• 线性层(Linear layer), 卷积层(Convolutional layer), 池化层(Pooling layer), 各类正则化(XNorm layer)
• 自定义layer
  • Attention layer, Transformer Block, Decoder Layer, ...