模型的训练/学习
- 目标:
- 猜个
- 评估误差:
- 根据误差,更新
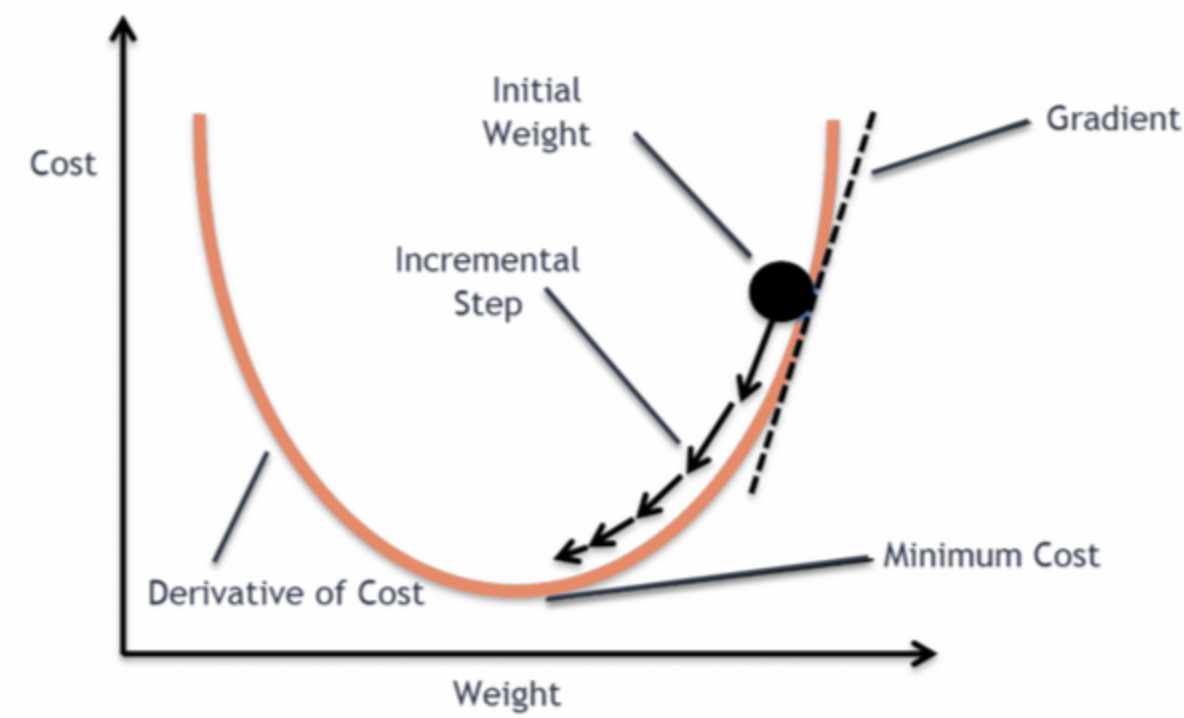
训练模型(搜索/开发参数)
优化目标:
梯度下降法 (Gradient descent): 求偏导(partial derivative)
-
- 通常深度学习模型
-
核心算法: 反向传播(backpropagation)
- 核心步骤: 针对优化目标
- 核心步骤: 针对优化目标
反向传播(backpropagation)
-
假设深度学习模型为
-
优化目标
-
链式法则展开:
-
偏导的构建
- 传统手工实现 v.s. 基于计算图的autograd
计算图:模型计算的DAG图
- 节点:表示变量(input, weight等)和操作(各种运算等)
- 边:表示数据的传递
- 前向传播:沿着边的方向计算
- 反向传播:沿着边的反方向计算梯度
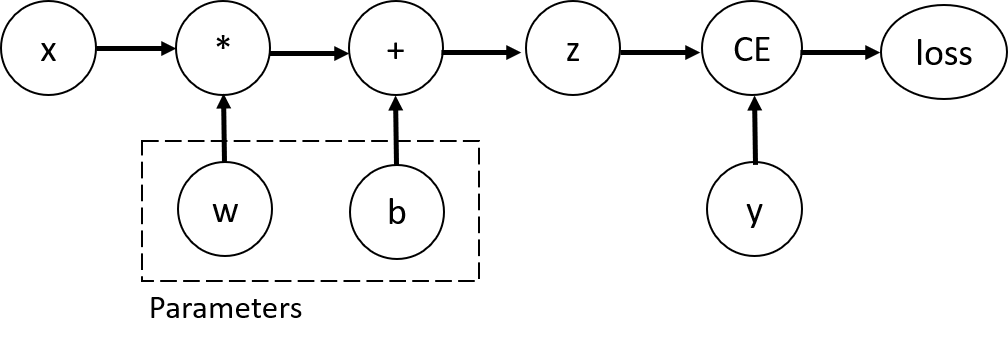
举个例子:线性层的反向传播
线性层:
损失函数:
前向传播:
- 输入:
- 输出:
反向传播(链式法则):
其中
自动求导:PyTorch的核心特性
- 计算图:PyTorch自动构建计算图
- 基于
nn.Module,Tensor以及用户实现的forward方法
- 基于
- 梯度追踪:在PyTorch中,Tensor对象设置
requires_grad=True即可启用对该Tensor的梯度计算 - 反向传播:
backward()自动计算梯度
Autograd的无感知使用
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
for epoch in range(100):
# 前向传播
y = net(x)
loss = criterion(y, target)
# 反向传播
optimizer.zero_grad() # 清零梯度
loss.backward() # 计算梯度
optimizer.step() # 更新参数
Autograd 概览(动态计算图)
- 动态计算图: 前向时即时构图,
requires_grad=True的参与者会被追踪。- 叶子节点: 叶子是直接由用户创建且需梯度的tensor,其梯度累积在
.grad - 非叶子节点:由运算生成的新tensor,比如
z=x+y, z中包含grad_fn,是用于记录的Function对象,描述生成该tensor的运算方式,以及反向传播时如何计算梯度
- 叶子节点: 叶子是直接由用户创建且需梯度的tensor,其梯度累积在
import torch
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
print(x.grad_fn) # None,因为x是叶子张量
print(y.grad_fn) # <AddBackward0>,表示 y = x + 2
print(z.grad_fn) # <MulBackward0>,表示 z = y * y * 3
print(out.grad_fn) # <MeanBackward0>,表示 mean 操作
- y.grad_fn =
:说明 y是通过加法操作得到的。 - z.grad_fn =
:说明 z是通过乘法操作得到的。 - out.grad_fn =
:说明最终输出是 均值操作的结果。
计算图抽象示意
out = z.mean() (grad_fn = MeanBackward0)
^
|
z = y*y*3 (grad_fn = MulBackward0)
^
|
y = x+2 (grad_fn = AddBackward0)
^
|
x (leaf, requires_grad=True, grad_fn=None)
常见反向节点名称对照(PyTorch)
- AddmmBackward: 对应 addmm 的反向(矩阵乘 + 偏置相加),是
nn.Linear/F.linear的核心反向- 典型梯度:
- 可能显示为
AddmmBackward0等后缀变体
- 典型梯度:
- TBackward: 对应
transpose的反向,是线性层实现里常见的辅助节点(例如W.t())。反传中将梯度再转回原始维度 - AccumulateGrad: 不是算子反向,而是“叶子张量梯度累加”节点。把传来的梯度写入叶子张量(如
Linear.weight/bias或requires_grad=True的输入)的.grad中,并按步累加
反向传播的启动过程
当执行out.backward()时,PyTorch 会从out.grad_fn出发,沿着计算图往回追踪,调用每个grad_fn对应的backward()方法,逐步计算出各个叶子节点(比如参数x)的梯度。
几个注意点:
- 叶子张量(用户定义的变量)的
grad_fn一般是None。 - 如果一个张量是通过in-place操作得到的,因为这可能会影响计算图的正确性,所以
grad_fn会变成AccumulateGrad或者触发警告。 - 在调用
.detach()或.data时,得到的新张量也不会有grad_fn,因为它被认为是从计算图中“断开”了。
工程视角看Autograd:你需要知道的
- 动态计算图:前向即时构图;非叶子张量有
grad_fn,叶子张量的梯度写入.grad。 - 基于向量-雅可比积(VJP):
backward()等价逐层执行- 原理提示:背后采用“反向模式自动微分”(向量-雅可比积,VJP)实现高效梯度计算;想深入可参考 PyTorch Autograd 文档:https://pytorch.org/docs/stable/autograd.html
工程视角看Autograd:你需要知道的
- 标量 backward:对标量输出使用
y.backward()- 反向传播需要一个起点,对标量来说,就是1
- 例如
y=model(x),假设y.shape=[batch,dim],直接调用y.backward()会报错,因为torch内部不知道到底该对哪个方向做反向传播
- 非标量 backward:对非标量输出使用
y.backward(gradient=v),v与y同形(shape)表示上游grad权重。
工程视角看Autograd:你需要知道的
- 线性层
- 计算图常见节点:
AddmmBackward(Linear/F.linear 反向)、TBackward(转置辅助)、AccumulateGrad(叶子梯度累积)。
- 训练循环要点:
zero_grad()防梯度累积;参数更新放优化器或no_grad();避免对中间结果原地修改。
工程视角看Autograd:你需要知道的
- 高阶/多次反向:按需使用
create_graph=True与retain_graph=True;默认一次反向后释放图。 - 性能与调试:AMP、梯度检查点、
torch.compile;结合 hooks 与 notebook 的图打印定位梯度流。
注:理论上可把 Autograd 看成“雅可比链式法则”的高效实现,理解这一点即可,不必掌握雅可比的形式化定义再上手工程实践。
Hook 示例
h = []
def log_grad(grad):
h.append((grad.mean().item(), grad.norm().item()))
out = net(x)
out.register_hook(log_grad) # 观察上游梯度
loss = criterion(out, y)
loss.backward()
梯度累积与清零
.grad默认累加;训练循环应先清零再backward()。
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
高阶梯度与图保留
- 二阶/高阶导:
create_graph=True构建可微分的反向图。 - 多次反传: 若复用同一前向,需
retain_graph=True。
g = torch.autograd.grad(loss, params, create_graph=True)
g2 = torch.autograd.grad(sum(p.sum() for p in g), params)
分离与禁用追踪
x.detach():把张量从当前计算图中分离,后续关于该结果的计算不会把梯度回传到被分离的分支。与原张量共享存储(谨慎原地写)。- 用途:
- 截断梯度(冻结某分支、teacher 模型前向等)。
- 缓存中间结果重复使用但不参与训练。
- 用途:
分离与禁用追踪
注意事项:
- 不要在训练前向外层包
no_grad/inference_mode,否则无法计算梯度。 detach()会打断梯度流,误用会让模型学不动;仅在确需截断时使用。- 分离张量与原张量共享存储,避免原地写引入隐性错误。
with torch.no_grad()::上下文内不记录计算图,不分配grad_fn/中间量,因此这些计算不参与loss.backward()。- 与反向的关系:在该上下文中产生的新张量,即使参与后续损失计算,梯度也不会通过它们回传(因为没有构图)。
- 用途:
- 纯推理/验证(配合
model.eval())。 - 统计/后处理(如 metrics、argmax/topk)。
- 无梯度的参数更新(如 EMA、手写优化步骤)。
- 纯推理/验证(配合
with torch.inference_mode():面向纯推理/部署的模式- 与反向的关系:不构图
- 跳过版本计数与视图跟踪,进一步减少元数据与一致性检查的开销;可视为只读、无梯度的快速前向
- 适用场景:离线/在线推理、模型服务、导出前的快速验证
- 与反向的关系:不构图
| 特性 | no_grad |
inference_mode |
说明 |
|---|---|---|---|
| 构图 | 关闭 | 关闭 | 两者都不记录计算图 |
| 版本计数/视图跟踪 | 保留 | 跳过 | inference_mode 更省内存/检查更少 |
| 内存/速度 | 省 | 更省/更快 | 大模型推理建议 inference_mode |
| 训练期使用 | 可用于局部(如指标、EMA) | 不建议 | inference_mode 仅用于纯推理 |
| 原地修改检测 | 有检查 | 检查更少/可能被绕过 | 训练期更安全用 no_grad |
A0简介:问题设定
- 线性变换:
- 形状:
- 损失:
Loss = (Y**2).sum()(标量,便于直接反传)
A0简介:梯度推导
- 上游:
- 参数: 合并批序
- 若有偏置
- 输入:
A0简介:代码
import torch
torch.manual_seed(0)
B,H,D,E = 2,3,4,5
X = torch.randn(B,H,D, dtype=torch.float64, requires_grad=True)
W = torch.randn(D,E, dtype=torch.float64, requires_grad=True)
Y = X @ W
Loss = (Y**2).sum()
Loss.backward()
grad_X_auto, grad_W_auto = X.grad.clone(), W.grad.clone()
G = 2 * Y.detach()
dW = X.detach().reshape(-1,D).T @ G.reshape(-1,E)
dX = torch.matmul(G, W.detach().T)
assert torch.allclose(grad_W_auto, dW, rtol=1e-6, atol=1e-6)
assert torch.allclose(grad_X_auto, dX, rtol=1e-6, atol=1e-6)
A0简介:调试清单
- 形状与展平:
contiguous()后再view/reshape,避免 stride 问题。 - 广播与偏置:
db对非通道维求和;检查维度顺序。 - 梯度累积: 多次
backward()会累加.grad,对比前先zero_grad()。 - 数值校验: 用双精度与
torch.autograd.gradcheck。 - 观测工具:
tensor.register_hook打印关键梯度的均值/范数。